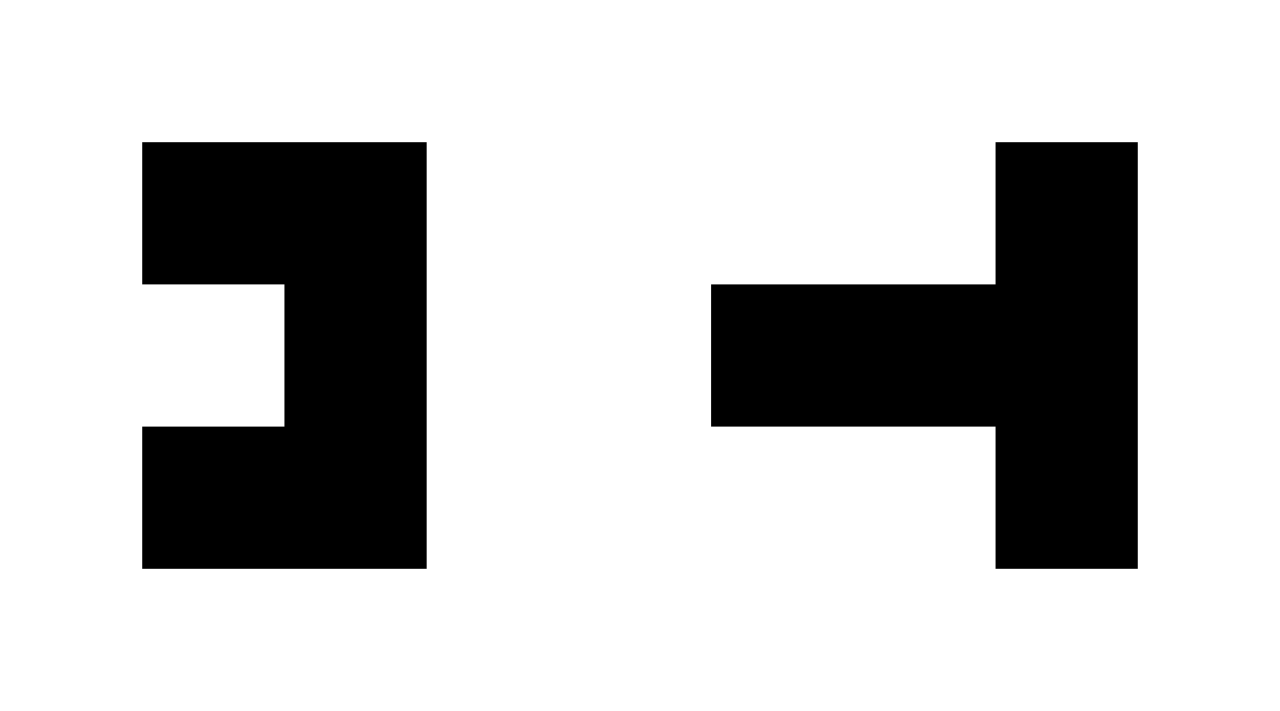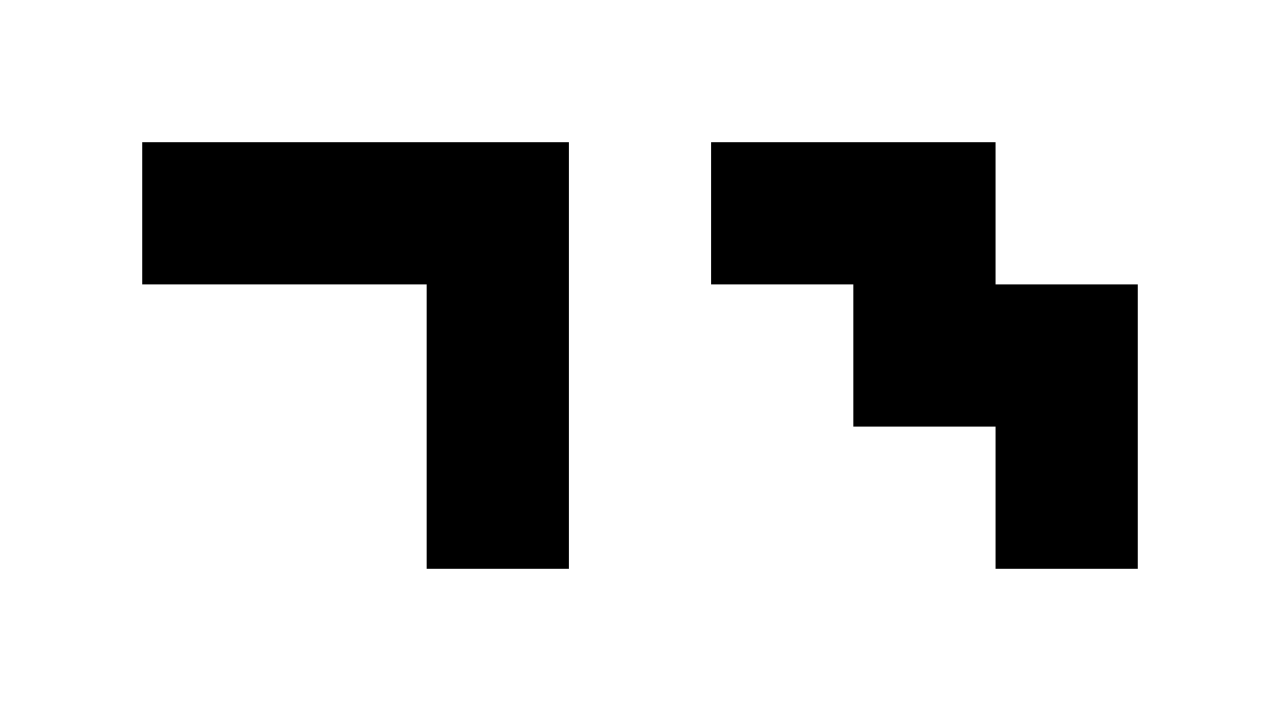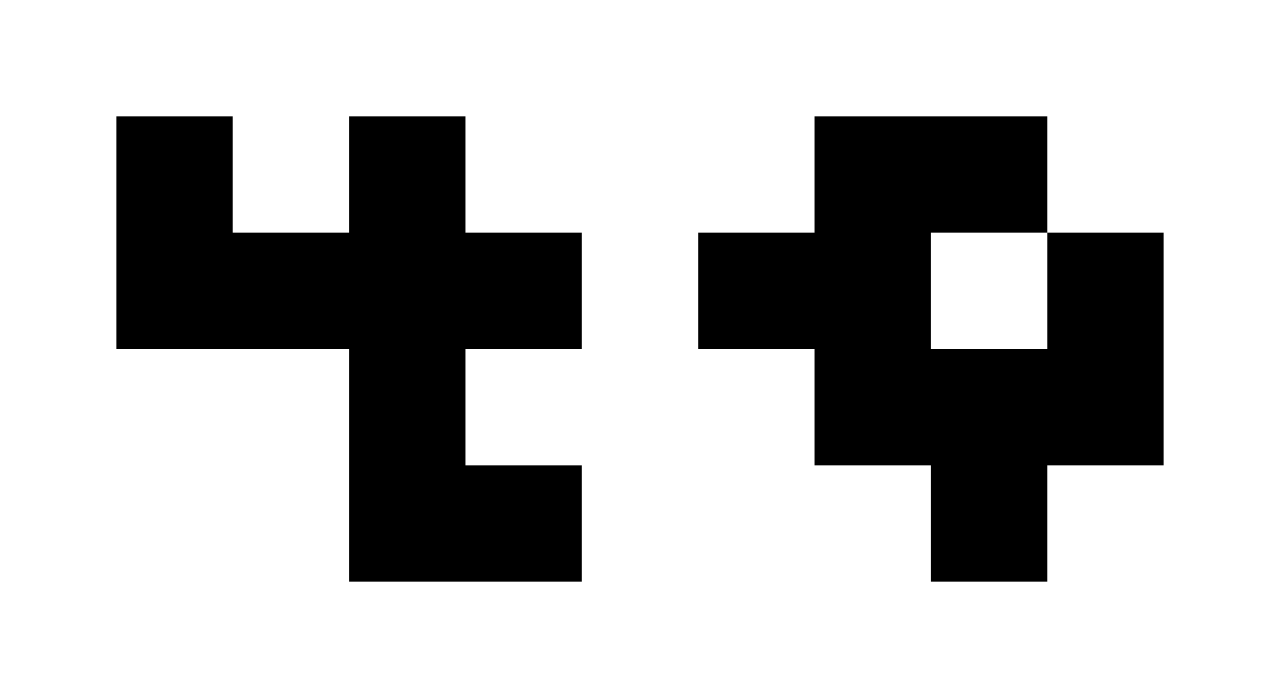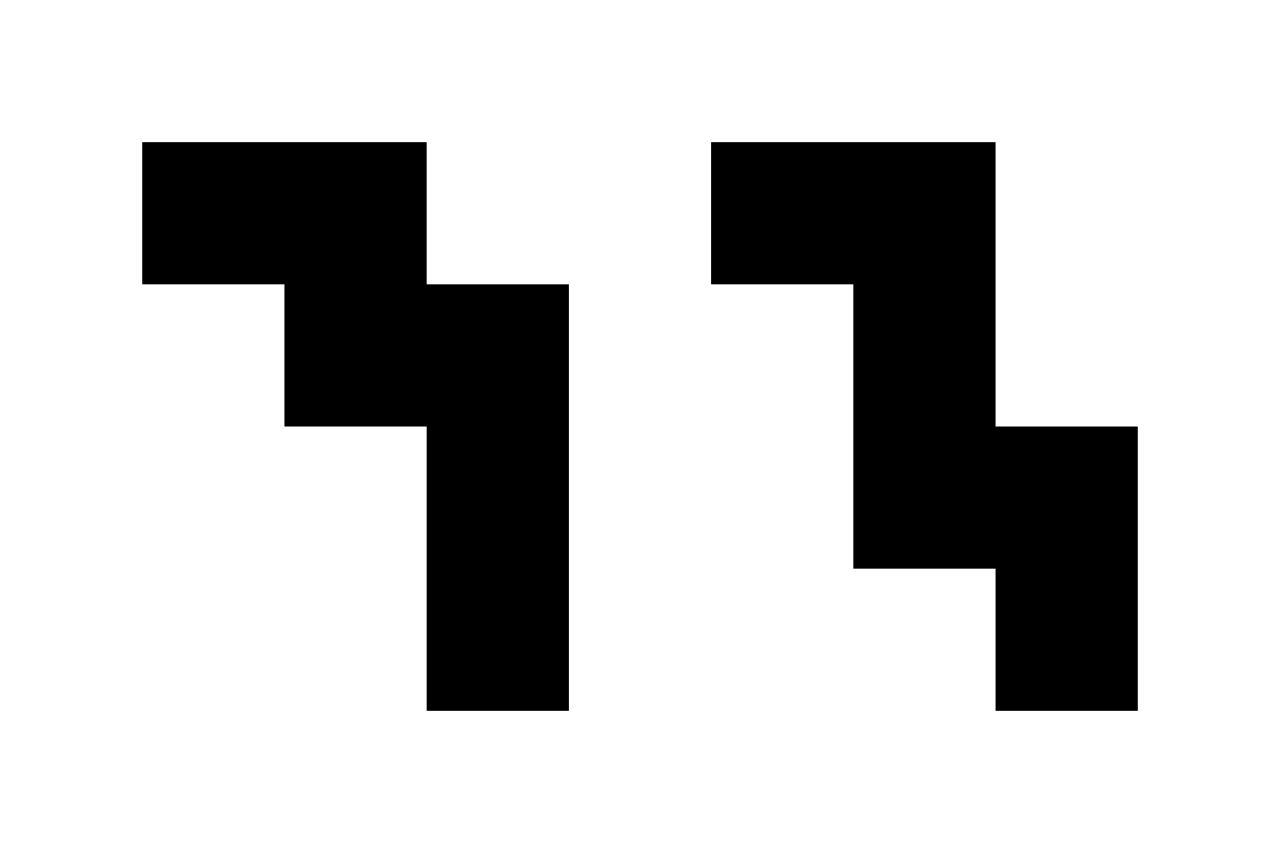polyominoes are shapes made out of orthogonally connected unit squares (like in tetris). I think they’re really fun, but one problem is that there really isn’t any established method for referring to them. lower-order polyominoes are generally referred to by letters that they resemble, but that doesn’t scale well. there are more polyominoes than letters.

so, here’s my system! full description under the cut, but here’s a spreadsheet with the names for all the polyominoes with up to nine squares, if all you want is the names of these shapes.

in this system, polyominoes are described extremely thoroughly according to several defining properties.

number of squares

this is the part that’s already well-established. a monomino has one square, a domino has two, a tromino has three, a tetromino has four, and so on. the numeral prefixes I’m using to generalize these established names are the same as in my base-naming system, so for example a twelve-square polyomino is a “dozomino”.

for a monomino or a domino, the number of squares alone is enough to uniquely describe the polyomino. for any higher order, you need a little more information.

symmetry group

this is one of my favorite parts of this system.

after the numeral prefix, there’s a suffix that indicates what symmetries the polyomino has. this suffix is broken into three parts.

starting from the right, the ending of the suffix indicates rotational symmetry. -o (polyomino) is the generic form, leaving rotational symmetry unspecified. -e (polyomine) means no rotational symmetry, -us (polyominus) means twofold rotational symmetry, and -on (polyominon ) means fourfold rotational symmetry.

before that, the middle part of the suffix indicates reflectional symmetry. -min- (polyomino) is the generic unspecified form, -m- (polyomo) means no reflectional symmetry, -mil- (polyomilo) means one axis of mirror symmetry, -mic- (polyomico) means two axes of mirror symmetry, and -dr- (polyodro) means four axes of mirror symmetry.

and finally (or I guess initially), the vowel at the start of the suffix indicates the alignment of the axis or axes of mirror symmetry, when relevant. -o- (polyomino) is generic, -a- (polyamino) means orthogonal axes, and -i- (polyimino) means diagonal axes.

in total, there are eight distinct symmetry groups a polyomino can belong to:

• asymmetric (polyome)
• one orthogonal line of mirror symmetry (polyamile)
• one diagonal line of mirror symmetry (polyimile)
• chiral twofold rotational symmetry (polyomus)
• two orthogonal lines of mirror symmetry (polyamicus)
• two diagonal lines of mirror symmetry (polyimicus)
• chiral fourfold rotational symmetry (polyomon)
• four lines of mirror symmetry (polyodron)

in some cases, the numeral prefix for the number of squares and this suffix for the symmetry group is sufficient to uniquely describe a polyomino. (for example, there is only one pentodron: the five-square polyomino shaped like a plus sign) however, most of the time you need more information than that.

stability

the stability of a polyomino is, in simple terms, the number of “non-load-bearing” squares in the pattern. how many of the squares could individually be removed while keeping the polyomino connected? this turns out to be a very useful thing to be able to refer to.

as an example, here are two pentamiles. they both have five squares, and one orthogonal line of mirror symmetry. the one on the left has two non-load-bearing squares (the two on the left side), and the one on the right has three (the one on the left, the one on the top, and the one on the bottom). you can check for yourself to verify that removing any other square from either of these will result in the remaining squares no longer being orthogonally connected.

so, the two pentamiles can be distinguished from each other by calling the one on the left the diadic pentamile, and the one on the right the triadic pentamile. in general, a polyomino with n non-load-bearing squares is n-adic, using the same kinda silly numeral prefix system as everything else.

but what about when this isn’t enough information either?

sides

here are the two pentimiles, both of which are diadic. they can be distinguished by counting how many sides they have: the one on the left is hexagonal, and the one on the right is decagonal. so, their names are the hexagonal pentimile and the decagonal pentimile.

counting how many sides a polyomino has isn’t as straightforward as you might expect due to some literal edge cases like this one:

this is a heptomino with a hole in it. how many sides does it have? I think most people would say it has ten sides, but you could also say it has six (ignore the hole), nine (there are nine vertices), or what I did and say it has eight sides.

I think this particular method of counting sides is more elegant mathematically (and computationally), which is why it’s what I’m using. also it’s fun!

holes

these are the two tesseragonal (sixteen sided) tetradic ennimiles. the one on the right has a hole in it, and the one on the left doesn’t, so the left one can be called the solid tesseragonal tetradic ennimile and the right one can be called the hollow tesseragonal tetradic ennimile.

for polyominoes with more than one hole, you add a numeral prefix to “hollow”, eg. bihollow, trihollow, tetrahollow, etc.

longest line

these are the two polyominoes that can be called an octagonal diadic hexomus. (they’re also both solid, but that’s not necessary to specify in this case because there isn’t a hollow octagonal diadic hexomus.)

these are distinguished by the lengths of their longest line of squares. unlike previously described parts of these names, this is relative, not absolute; all that matters is that the one on the left’s longest line is shorter than the one on the right. in this case, these are called the minor octagonal diadic hexomus and the major octagonal diadic hexomus.

there are naturally cases where you need to distinguish between more than two longest-line lengths, so these two words can be supplemented with additional words as necessary:

• minor, major
• minor, medial, major
• subminor, minor, major, supermajor
• subminor, minor, medial, major, supermajor
• subminor, minor, superminor, submajor, major, supermajor
• subminor, minor, superminor, medial, submajor, major, supermajor
• subminor, minor, superminor, submedial, supermedial, submajor, major, supermajor
• subminor, minor, superminor, submedial, medial, supermedial, submajor, major, supermajor
• bisubminor, subminor, minor, (…) major, supermajor, bisupermajor
• trisubminor, bisubminor, subminor, minor, (…) major, supermajor, bisupermajor, trisupermajor

and so on from there, including “medial” only when there’s an odd number of different longest-line lengths that need to be distinguished.

bounding area

these are the three octagonal diadic hexomes. the one on the right has a longer longest line than the other two, so it’s the major octagonal diadic hexome , but the other two (which are both minor) can be further disambiguated using their bounding area.

the one on the left fills a three-by-three rectangle, and the one in the middle fills a three-by-four rectangle. in this sense, the left one is smaller than the middle one, so they are respectively named the small minor octagonal diadic hexome and the great minor octagonal diadic hexome.

just like minor and major, small and great are part of a larger set of relative terms, and which ones are used depends on how many distinct bounding areas are being compared.

• small, great
• small, middle, great
• smaller, small, great, greater
• smaller, small, middle, great, greater
• smallest, smaller, small, great, greater, greatest
• smallest, smaller, small, middle, great, greater, greatest
• smallest, smaller, small, smallish, greatish, great, greater, greatest
• smallest, smaller, small, smallish, middle, greatish, greater, greatest
• bismallest, smallest, smaller, small, smallish, (…) greatish, great, greater, greatest, bigreatest
• trismallest, bismallest, (…) bigreatest, trigreatest

and so on, using “middle” when there’s an odd number of areas being compared.

aspect ratio

these are the two smaller minor dozagonal diadic octomes. their bounding rectangles have the same area (twelve square units), but the one on the left is three-by-four and the one on the right is two-by-six. to convey this, they’re called the broad smaller minor dozagonal diadic octome and the narrow smaller minor dozagonal diadic octome.

specifically, “broad” means closer to a square, and “narrow” means more elongated. these terms are further extended in the same way as small and great, with “intermediary” as the equivalent of “middle”.

last resort

if two polyominoes have all of these things in common, they’re pretty dang similar shapes.

these are the two great decagonal diadic hexomes. they’re basically the same shape, but they’re still distinct. what I’ve decided to do when this happens is to just number them, semi-arbitrarily. the one on the left is the primary great decagonal diadic hexome, and the one on the right is the secondary great decagonal diadic hexome.

but of course, what order should they go in? I think the most natural thing to do is to convert the polyomino into a binary number, then sort numerically. since in order to get to the point where this step is necessary polyominoes are guaranteed to have the same bounding box, there’s no need to indicate where the different rows start and end; you can just read off all the squares one after the other.

in this example, these two polyominoes are 001 001 011 110 and 001 011 010 110, reading from the bottom row up (with the “origin” placed at the bottom left corner).

one minor issue with this is that a single polyomino can have up to eight distinct orientations. so, to convert it into a number, you first need to pick which orientation is “canonical”. the solution I went with is to use whichever orientation of the ones where the shorter side of the bounding box is the width corresponds to the lowest number in binary.

a more significant issue with this, which I haven’t really solved, is that there are still so many dang polyominoes.

these are the thirty-seven distinct greatish minor solid dozagonal triadic ennomes. while the vibes of these shapes are indeed very similar, it would be nice to be able to distinguish between them in some way other than just numbering them one through thirty-seven (as fun as using my base-naming system to generate words like “bikery” for the 26th one may be).

closing thoughts

the names this system generates are by no means practical or convenient, but they are highly descriptive, which was my main goal. regardless, for practical purposes just inserting an image inline with text is almost always a better way to refer to higher-order polyominoes than any naming scheme.

there are many important things that this naming system does not describe which could hypothetically be incorporated into a derivative system. one worth noting is whether or not a given polyomino can tile the plane. as it turns out, figuring out if an arbitrary polyomino can tile the plane is computationally really hard, so it would be unsuitable for something like this.

this system only describes “free” polyominoes, where mirror images count as the same shape. following tetris rules, however, those chiral pairs (such as the “S” and “Z” tetrominoes, both of which are called a “tetromus” by my system) should count separately. my recommended solution to this is to refer to the canonical orientation as the “left-handed” one and its mirror image as “right-handed”.